알파 베타 가지치기/alpha-beta pruning
Alpha-Beta Pruning
미니맥스 알고리즘의 단점으로 가장 대표적인 가능한 멀리까지 예상할수록 더 나은 결과를 얻을 수 있지만, 이러한 성능을 가지려면 막대한 시간과 공간을 차지하게 된다는 것입니다.
바둑이나 오목의 의 경우 19*19 칸에서 이뤄지게 되는데 한수앞을 더 예상하기 위해서는 (19*19)(19*19-1)(19*19-2)(19*19-3)...
이렇게 거의 19*19 만큼의 경우가 곱해지게 됩니다. 극단적인 예로 엄청난 공간을 가지고 있는 인공지능이기에 기하급수적으로 추가되는 공간을 소화할 수 있다고 해도 바둑은 제한시간이 존재하기 때문에 한 수를 두는데 모든 시간을 다 차지해 버릴 수도 모릅니다.
하지만 잘 생각해보면 바둑에서 상대방 흑돌이 중앙자리에 돌을 놓고 내 차례가 되었을 때 제정신이 아니고선 양쪽 끝자리에 내 돌을 두진 않을 것입니다. 이런 개념으로 진작에 가능성이 없는 경우는 미리 제거하자고 하는 게 바로 알파-베타 가지치기입니다.
이렇게 미리 쓸모없는 가능성들을 제거함으로써 시간과 공간의 낭비를 줄일 수 있습니다.

미니맥스 알고리즘의 진행대로 가면서 알파베타 가지치기를 해보겠습니다. 검색방식은 깊이 우선 탐색입니다.
1. 4번 줄은 제 차례이기 때문에 5 6 - 7 4 5 - 3 - 6 - 6 9 - 7 - 5 - 9 8 - 6이라는 경우들을 선택했습니다.
2. 3번 줄 상대방의 차례에서 5,6 중 작은 수 5를 택하고 7,4,5를 차례로 탐색하기 시작합니다. 7을 탐색하고 4를 탐색하고 난 뒤 5를 탐색하기 전에 생각합니다.
만약 4보다 높은 수가 나온다면? -> 상대방이 택하지 않고 최소의 수인 4를 택한다.
만약 4보다 낮은 수가 나온다면? -> 상대방은 4보다 낮은 이 수를 택할 것이다 -> 하지만 다음 내 차례에서 5보다 낮기에 내가 택하지 않는다.
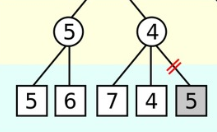
즉 어떤 숫자가 나오던지 상대방 또는 내가 택하지 않게 됩니다. 그래서 5를 검색하기 전에 가지치기를 해버립니다.
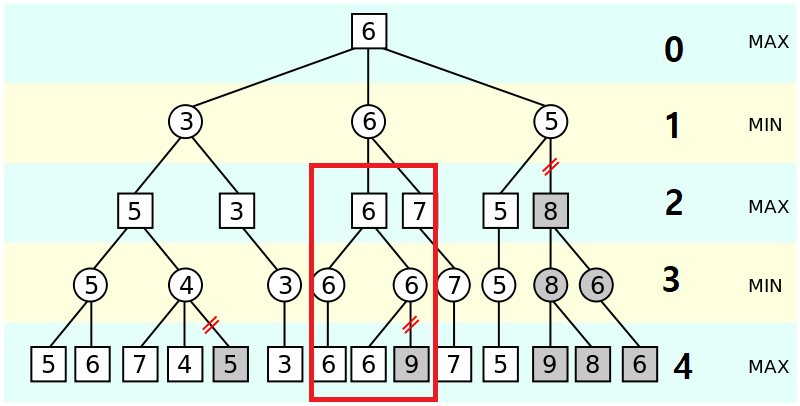
3. 이제 빨간 박스 안의 상황을 보겠습니다. 첫 번째 6은 다른 선택이 없어 6이 선택되었고 6, 9가 있는 노드 중 6이 들어 있는 노드를 탐색했습니다. 이제 9가 들어있는 노드를 탐색하기 전에
만약 이 노드가 6보다 높은 수가 나온다면? -> 상대방은 이 숫자를 택하지 않고 이전에 검색된 6을 선택한다.
만약 이 노드가 6보다 낮은 수가 나온다면? -> 상대방은 6보다 낮은 숫자를 택하게 되지만 다음 내 차례에서 이 숫자를 택하지 않는다.
즉 만약 가지치기하지 않고 9가 탐색된다면 상대방은 6, 9 중 6을 택하게 됩니다. 반대로 6보다 낮은 수 예를 들어 3이 탐색되었다고 가정하면 상대방이 3을 택하게 됩니다. 하지만 다음 내 차례에서 6, 3중 6을 택하게 됩니다.
다시 말해서 어떤 수가 나오던지 상대방 혹은 내가 택하지 않게 되기에 검색할 필요가 없는 것입니다.
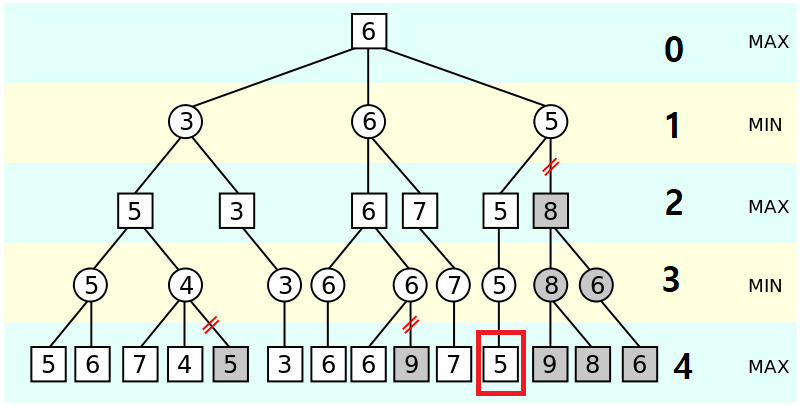
4. 현재 깊이 우선 탐색을 통해 빨간 박스까지 검색을 했습니다.
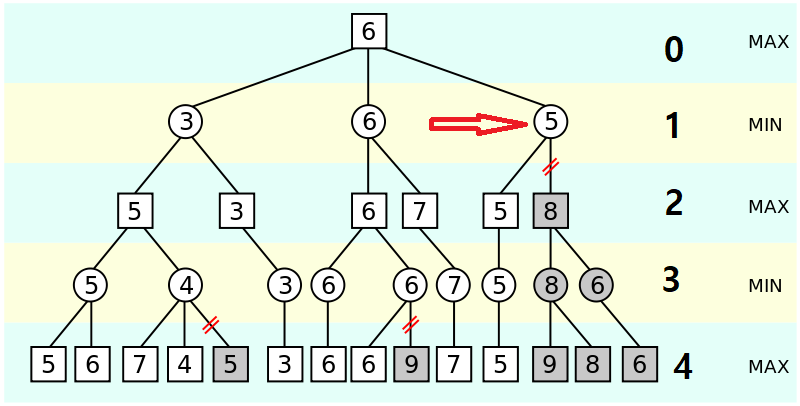
다시 빨간 화살표가 표시된 노드까지 올라가서 8이 들어가 있는 노드부터 검색해보려 합니다. 하지만 8이 들어간 노드가 화살표로 표시된 노드인
만약 5 보다 크다면? -> 상대방의 차례에서 선택하지 않고 이전에 검색된 5를 택한다.
만약 5 보다 작다면? -> 만약 8이 아니라 2라고 가정했을 때 상대방은 5, 2 중 2를 택하게 되지만 다음 내 차례에서 이미 검색된 3, 6 보다 작은 수이기에 내가 선택하지 않는다.
다시 말해서 5보다 큰 수는 상대방이 선택하지 않고 5보다 작은 수는 다음 차례의 내가 선택하지 않는다.
이렇게 알파 베타 가지치기의 진행과정을 살펴보았습니다. 상대방이 택하지 않거나 내가 택하지 않기에 어떤 수가 나와도 선택될수 없다. 이것이 알파 베타 가지치기의 개념입니다.
자바 구현 코드
// Java program to demonstrate
// working of Alpha-Beta Pruning
import java.io.*;
class GFG {
// Initial values of
// Alpha and Beta
static int MAX = 1000;
static int MIN = -1000;
// Returns optimal value for
// current player (Initially called
// for root and maximizer)
static int minimax(int depth, int nodeIndex,
Boolean maximizingPlayer,
int values[], int alpha,
int beta)
{
// Terminating condition. i.e
// leaf node is reached
if (depth == 3)
return values[nodeIndex];
if (maximizingPlayer)
{
int best = MIN;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
false, values, alpha, beta);
best = Math.max(best, val);
alpha = Math.max(alpha, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
else
{
int best = MAX;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
true, values, alpha, beta);
best = Math.min(best, val);
beta = Math.min(beta, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
}
// Driver Code
public static void main (String[] args)
{
int values[] = {3, 5, 6, 9, 1, 2, 0, -1};
System.out.println("The optimal value is : " +
minimax(0, 0, true, values, MIN, MAX));
}
}
// This code is contributed by vt_m.Output :
The optimal value is : 5
'→ My Meta+IT > JAVA Source' 카테고리의 다른 글
| Multi-threaded chatting Application in Java (0) | 2022.12.06 |
|---|---|
| 이클립스(eclipse IDE) 오라클 클라우드(Oracle cloud) ojdbc11.jar database 연결 접속 성공 (0) | 2022.07.08 |
| MiniMax 미니맥스 알고리즘+JAVA 예제 코드 (0) | 2022.02.09 |
| HeidiSQL | MariaDB에 접속하는 방법 (0) | 2021.12.21 |
| MariaDB 다운로드 설치 (0) | 2021.12.21 |




댓글